SOLUTION:

If you are standing directly on the north pole and you walk one mile south, then one mile west, then one mile north, you will arrive back at the north pole. It would look something like this:
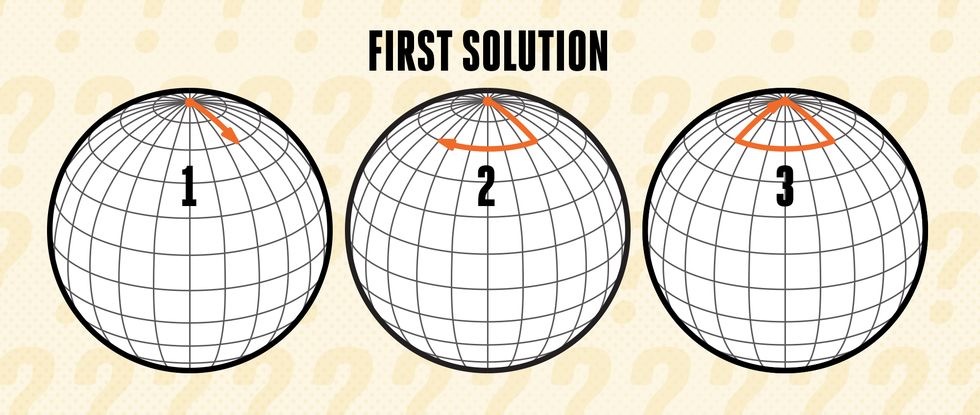
But there is a more nuanced solution to this problem as well. Imagine a circle with a 1-mile circumference that has the south pole at its center. If you were to start one mile north of this circle, you would travel one mile south, one mile west all the way around the circle, and then one mile north back to your starting point.
In fact, you could start anywhere that is one mile north of the circle around the south pole. (In the diagram, the orange circle has a 1-mile circumference, and you could start anywhere around the thick black latitude line.)
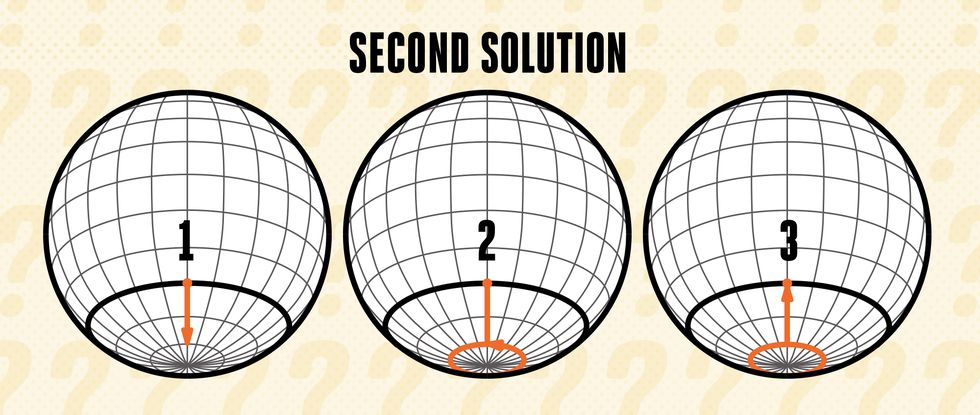
And the solutions don’t stop there. Imagine that the circle around the south pole has a circumference of 1/2 mile instead of 1 mile. If you were to start one mile north of that 1/2-mile circle, you would travel one mile south, one mile west around the 1/2-mile circle twice, and then one mile north back to your starting position.
If the circle were 1/3-mile, you could still start one mile north of it, and you would travel around the circle three times. The same is true for any fraction 1/n where n is a positive integer, and the result is that you walk around the circle n times. If the circle around the south pole is only a tenth of a mile, you can still start one mile north of it, walk one mile south, one mile west around the circle ten times, and then one mile north back to your starting position.
So there are an infinite number of solutions.









